all the code, numeric results and images related to this post are at https://github.com/davidedc/Die-and-matchsticks-simulator
Summary
The “die and matchsticks” game is presented in Goldratt’s best-seller “The Goal” as an example of subtle unintuitive behaviours of a pretty general “chain of workers” system. As the book analyses the outcome of the game, the reader’s intuition is quickly shown to be false. However, in the (perhaps necessarily quick) presentation and examination of this game, something goes amiss in regards to how the intuition that readers get from the presentation (unconstrained inventory) is *actually correct*. It’s an (unstated) constraint (limited inventory) that actually causes the reader’s intuition to fail. I’m going to re-visit the game and make the constraint explicit, and show exactly which part of the reader’s intuition is correct, and which part fails and why.
Introduction
“The Goal” by Eliyahu M. Goldratt is business book in the style of a thriller, published in 1984. The protagonist is in a pinch to save his factory (with a side story of marriage crisis), and business operations management ideas are presented during the unfolding of the plot.
This is an immensely successful book (it sold in the millions) that also influenced a number of program and project management methodologies in routine use today (e.g. Kanban).
The success of this book comes from the ability to popularize to a vast business audience in the services industry (and a growing IT industry) elements that came from previous operations settings such as supply chains and factory plants. Some of these ideas from operations management resonate with daily intuition (for example that a chain of processes can only progress as fast as the slowest step), but their ramifications are tricky enough that they deserve a systematic look.
The format of the presentation was novel, and even more importantly the description of team dynamics that cause sub-par decision-making is spot-on (“what do you mean that we don’t care about the productivity of this machine???”). In fact I think that this aspect alone justifies buying the book: it really fleshes out all-too-common pitfalls in management routines e.g. looking at metrics of efficiency that are too narrow, ignoring the cost of inventory, looking for productivity increase where it doesn’t matter, etc.
The formalisation of these ideas started with queuing theory in the early 1900s to help analyse the first “mega”-scale applications of the 20th century, for example in sizing telephone networks (how many calls are likely to be connected at any one time?), and later on in the 20s to analyse the first huge production plants. It is certain however that practices regarding inventory management and staged processes are pretty much lost in time (renaissance and even before then), as several complex global supply chains (e.g. complex transportation and exchanges of perishable goods such as food and fabrics, and silk expecially) and modern factories existed well before “modern times”.
The “die and matchsticks” game
Enough as an introduction, let’s jump to the matter at hand. Goldratt presents a game in Chapter 14, the “die and matchsticks” game. The heart of the game is this: suppose you have 5 robots taking tokens from a bowl to its left (if there are any) and putting them on a bowl to its right. The first robot takes from an infinite bowl, so the first robot always has tokens to move to its right. Also, the robots have a random efficiency, so they can transfer a random number of tokens from 1 to 6 (a dice roll) at each take. It’s important to realise that robots can only pick up tokens if they are there: if a robot wants to pick up 6 tokens but there are only 2 in its “source” bowl, it will only pick up the two available.
Is your intuition right?
So, here we have a chain of robots all trying to move tokens to the right, and because of the “random pick between 1 and 6”, we can safely say that on average the first robot will move 3.5 tokens at each turn. We’d be tempted by some sort of “induction” to think that since all robots will on average behave the same, that the whole chain will have the same overall efficiency and will hence move 3.5 tokens at each turn on average.
You’d be right in fact.
But, according to Goldratt, you’d be also wrong. Goldratt is right in some sense, however I feel that he goes a little heavy-handed and fails to shade-in some details on why the intuition is actually fundamentally correct, and only an unstated contraint makes it incorrect. I’ll endeavour to fill-in those parts here.
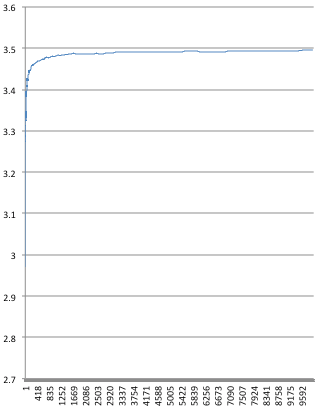
Let’s quickly settle the issue with a simulation so we build on some results. I’ve added the code for simulation here. With this simulation, we see that we start “low”: after 100 rounds the throughput is 2.97, significantly less than 3.5. However after 4600 rounds it’s 3.40…, after 311100 rounds it’s 3.490…, after a million rounds is 3.495…, after 40 millions is 3.4990…, after 1.6 billions is 3.49990… and so on converging to 3.5.
However, Goldratt heavilly weighs-in on the other thesis, side-stepping the “correct” part of the intuition, which I think is a pity because it makes it difficult to pin-point precisely why practically “chained” systems indeed show lower throughput than their parts.
Let’s zoom-in the take-away from Goldratt: “I look at the chart. I still can hardly believe it. It was a balanced system. And yet throughput went down. Inventory went up.” He then also shows how the flow of tokens is very uneven.
Out of those three takeaways, the ones about inventory and flow are airtight: the amount of tokens in the system can go up a lot and vary considerably with time (more on this later). However the one about throughput is misleading: it’s just an accident that in his play he observed decreasing throughput. In other plays he could get the opposite result, and in the long run he would have *certainly* observed increasing throughput.
So how do we have to interpret Goldratt’s conclusions?
Goldratt’s conclusion is correct in case of small inventory – which is a fundamental constraint that is not highlighted in the setup of the “die and matchsticks” game, and the true crux of why throughput is far from the ideal in real systems. I read the description of the game carefully: Goldratt tells us even the *type* of the matches (which we assume doesn’t influence the behaviour and analysis of the system), but never he mentions that the bowls’ limited capacity is a fundamental aspect of the game as opposed as being an accident of the particular instantiation of the concept (otherwise we migth as well call into question whether the finite number of matches available or the limited number of rounds played is also a factor). Besides, with each bowl reasonably being able to hold 100 matchsticks, the throughput in my simulation reaches 3.385 at the 2900th round, well above the 2.0 throughput shown in the book.
Why is the “small inventory” constraint critical? Because in that case we’d have two (symmetric) situations where robots will operate less efficiently:
- as soon as a bowl is full, a robot will have to stop adding tokens, until the next robot catches up. And because we know that *any* bowl will eventually get full (just because of streaks of bad luck that are inevitable in the long run), then we know that robots WILL have to pause and skip a turn every now and then. And hence we know that although in theory the robots move 3.5 tokens per cycle, in practice they won’t, because of the unfavourable runs: they’ll just have to skip tokens at some point.
- symmetric case: when we limit the amount of tokens in a bowl, we can incur more often in the case where the robot on the right might have taken more tokens than the ones available if the bowls were of infinite capacity. Again, skipped tokens.
As shown, larger inventories avoid the problem, and result in a throughput that converges to the one of the individual robots. However, as described in many points in the book, in practice a) inventories have costs and b) large inventories cause high lead time (the time it takes for a token to pass through the system) which is a big problem for perishable goods and “time to market” considerations.
How much inventory do we need to get good throughput?
In this analysis we’ve seen that the amount of inventory is critical: small inventories (small bowl sizes) produce terribe throughput (any unlucky run is going to cause “bowl too full” or “not enough tokens” problems, which reduce the number of tokens that robots move), and infinite inventory (infinite bowl size) produce ideal throughput over time. So what happens in between? Is there a bowl size that is practically OK? Do we get to a point where being able to hold more tokens doesn’t help the thoughput very much?
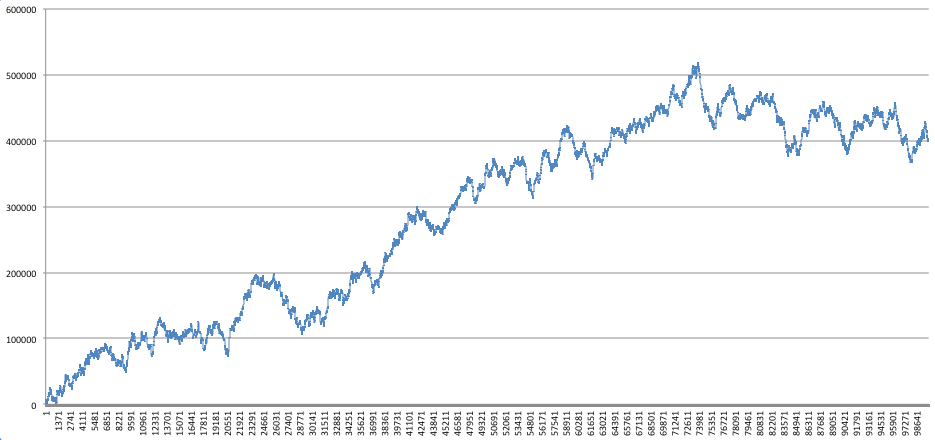
Indeed there is such a curve, but it’s not really a curve, it’s more like a random walk: the inventory size in such random process can be arbitrarily high (although with correspondingly low probability). This is the graph of the inventory size in a simplified simulation where there are two robots (instead of 5) and robots can only pick up 1 or 2 tokens (instead of 1 to 6). This reduced simulation obviously suffers no loss of generality compared to the original, but it’s quicker to run over 100 billion rounds. (the source code for this reduced simulation is also in the repo here).
It is absolutely staggering to see how such a simple system can generate an inventory of half a million tokens. The throughput at the 100th billion round is 1.499996312683127 (converging to 1.5 in this case).